Multi Robot Control and Planning

January 14, 2017

Overview

For my winter quarter project in the MSR program, I am seeking to simulate multiple wheeled robots to exhibit classical swarm robotics behaviors, such as leader follower formations. This is my first endeavor in implementing concepts of robotic control and trajectory generation. I utilize a centralized approach to broadcast velocity commands to each robot from a central computer.

Preliminary results indicate promise in trajectory following with circular trajectories, as well as shape formation with collision detection/avoidance. The latter came as an unexpected surprise when I was testing my collision detection algorithm originally intended for trajectory following application.

Implementation

The project package can be found at the following link.

I structure the nodes as follows:

Please note that the above image represents the general sequence of node operation, and that the names of the topics and nodes themselves change with the specific application being considered.

A brief overview of how the nodes operate is given as follows: The velocity controller subscribes to the pose_est topic, retrieves the pose estimate, and calculates the velocity control law to return a linear and angular velocity. This is then published to the cmd_vel topic that the integrator subscribes to, which is then used to perform Euler integration to return an updated pose estimate. Please refer to the next sections for a more detailed discussion of the theoretical underpinnings, as well as specific implementation considerations.

I utilize custom message types, a list of Pose2D messages and a list of Twist messages for publishing/subscribing pose and velocity related messages for every robot. Doing this enables the integrator and controller node to have access to every robot’s pose and velocity information at any given time. This is useful for collision detection/avoidance considerations.

Trajectory Following Control

In this example, my goal is to demonstrate leader-follower formation behavior. That is, each robot follows its defined predecessor with one robot being the “leader” who follows the defined trajectory.

I followed the approach set forth by Luca et. al, where they derive a globally asymptotically stable nonlinear control based on Lyapunov stability analysis. The control law is presented as follows:

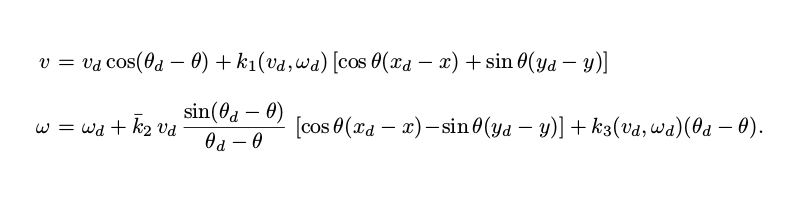
where k1 and k3 are equivalent gain functions, and \bar{k2} is constant:

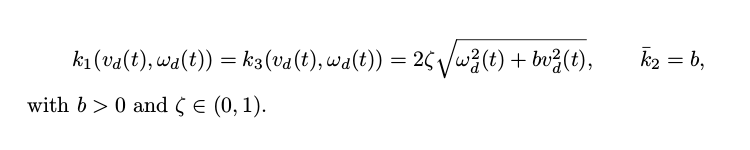
Further details about the control law can be found in the paper, which I point to in the references [1].

For implementation, three components are particularly crucial: phase variables, collision detection, and timers.

Phase variables are introduced as a means of introducing artificial delay so that each robot will follow its predecessor at a fixed distance. I define a scaling factor to allow for real-time adaptation of how close each robot is to another.

I implemented a relatively simple collision detection methodology, involving the following steps (for one robot relative to the rest of the robots):

1) Define a "safety" bounding box around each robot based on the distance it would have traveled with maximum velocity over the defined time step

2) If there are robots present in this bounding box, reduce linear velocity by a scaling factor, while increasing the angular velocity.

3) The angular velocity is increased on all robots, in such a manner that they rotate away from each other, then drive away without collision.

Timers are a useful tool which allow for a higher degree of control over when the callback functions are executed. I have attempted to implement a timer for trajectory generation so that it is slower than the main control loop (integration-control as seen previously), so that trajectory following may be more stable. This is an ongoing effort.

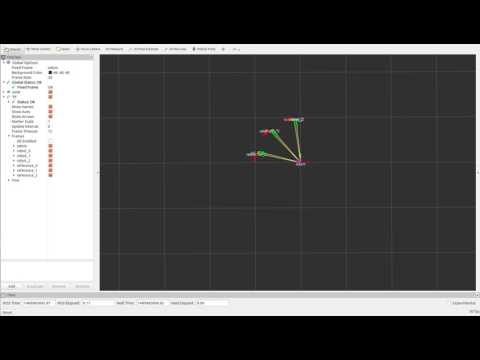
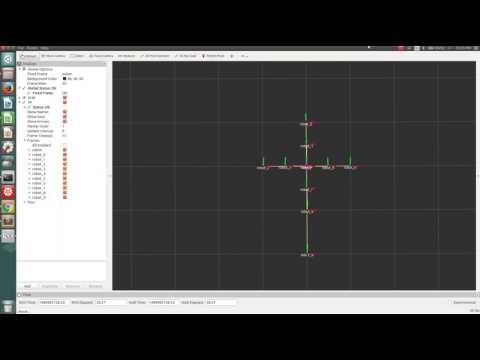
The RViz visualization shown hereafter depicts the robots’ tf frames, moving relative to a fixed ‘odom’ frame.

Please see the following video for preliminary results.

Challenges/Improvements

Challenges I encountered were mainly with debugging- specifically isolating where the issues could be. I had some initial struggles writing my angle wrapping functions, and it wasn’t until they were tested with various edge cases that I developed more confidence that those were not the source of my issues. It turned out ultimately that my issues were related to ROS related timing issues, which were mitigated with introducing ROS Timers.

Some immediate improvements I seek to implement include more robust timers to enable tunable control frequencies, since the existing solution may not fare well in other reference trajectories. I also intend to implement runtime parameters such as number of robots, control frequencies, the option of choosing a reference trajectory type. These will make future testing iterations much faster. I also hope to add in keyboard UI that enables the user to specify features such as start/stop times for the simulation, phase variable control. Additional features that would make this project interactive would be to introduce a means to arbitrarily define a reference trajectory, such as joystick control.

Shape Formation Control

Shape formation is accomplished by specifying initial and goal pose information for each robot. Each robot will navigate to its goal pose by the method outlined below, while attempting to avoid each other on the way.

As previously mentioned, shape formation with collision detection showed initial success owing to the implementation of the aforementioned collision detection. I use the following methodology in defining the velocity control law to drive each robot:

1) robot will turn toward the angle such that it is facing the desired goal position, with feedback proportional control- linear velocity is zero, while angular velocity is nonzero

2) robot will drive toward the desired goal position, with feedback proportional control- linear velocity is nonzero, while angular velocity is zero

3) robot will perform a final turn, so that it matches the desired goal orientation, with feedback proportional control- linear velocity is zero, while angular velocity is nonzero

Step 2) incorporates the collision detection/avoidance step by modifying the linear and angular velocities with the similar approach to the original collision detection/avoidance heuristic. Angular velocities are now nonzero in order to turn away from the heading angle that would otherwise induce a collision. Linear velocities are decreased as before.

The RViz visualization shown hereafter depicts the robots’ tf frames, moving relative to a fixed ‘odom’ frame.

Please see the following video for preliminary results.

Challenges/Improvements

I had implemented tolerances at each turn-drive-turn phase, in order for the feedback proportional control to terminate at an “appropriate” point. I loosely define what “appropriate” means because proportional control should theoretically oscillate, but still have non-zero steady state error. Implementing an additional integral term for PI control may be an option to consider.

I also assume that collision only occurs when in the “drive” phase, so a more robust collision avoidance method would be worthwhile to consider in examples including, but not limited to, where collision can occur by two robots rotating into each other.

Running the Simulation

To run the two examples, please type in the following commands:

Following a circular trajectory:

$ roslaunch winter_project trajectoryfollowing.launch

Shape Formation:

$ roslaunch winter_project shape_formation.launch

Work in Progress/Future Goals

I am concurrently building real differential drive robots to validate my simulations. To communicate wheel motor commands, such as wheel velocity and direction, I intend to utilize XBee communication. A camera will be mounted overhead in such a configuration that, ideally, the pose of every robot can be transmitted to the central computer at any given time.

Experimental efforts also introduce new problems to consider such as being able to handle missing robots. If the computer doesn’t know the pose of one robot at some instant, that robot would not know which instructions to follow at that point. Other robots may risk driving into it. A few considerations exist, such as taking its previous velocity and extrapolating a path until the robot is detected again.

Immediate goals I have to set up the hardware side of my project include: enabling AR tag tracking to do automatic tag assignment based on initial least squares error.

This project is a work in progress, please come back for future updates.

References

[1] A. De Luca, G. Oriolo, M. Vendittelli. “Control of Wheeled Mobile Robots: An Experimental Overview”, https://link.springer.com/chapter/10.1007%2F3-540-45000-9_8